While reviewing a colleague’s work I had a knee-jerk reflex to complain about the use of min() as an estimator for the running time of a program.

Specifically, during an experiment a complex workload was measured multiple times; unfortunately, in a subset of the measurements a few of the caches were cold and the running times were artificially high when compared to expected condition, thus the minimum of the measurements was chosen as the experiment output in order to avoid skew from these outliers.

Intuitively I figured out this approach would skew the results towards lower values, especially when increasing the sample size (number of measurement) in each experiment. While not great, this is not necessarily tragic, since a persistent bias still allows you to compare results and determine if running time improved or not. But since I didn’t exactly know what to expect in terms of precision (i.e. the variance acoss multiple experiments), I ran some empirical tests.

I’m not going to make a story out of this, so I’ll spell the findings out: min() is horrible both in terms of accuracy and precision for measurements following a normal distribution. However running times don’t follow a normal distribution but a positive skewed distribution¹ which makes min() perform unexpectadly well.

I started out with a large number of recorded running times for the convert tool from ImageMagick on a JPEG to PNG conversion job. I then fitted a normal and a Weibull distribution to the data to extract the parameters.

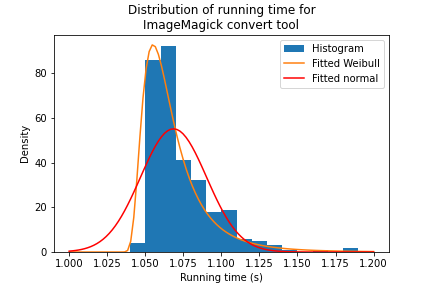
For each distribution an experiment consisted of generating SAMP_SIZE random numbers and aggregating the output with both min() and mean(). Each experiment was repeated 10000 times and the results were recorded. No other outliers (e.g. cold cache situation) were injected as these can be worked around in real scenarios.

Obviously when the sample size is 1 then both min() and mean() perform identically.

Execution time modeled by a normal distribution

As expected for a normal distribution, min() starts having a stronger bias when we increase the sample size. This is intuitively true as drawing more values increases chances of drawing smaller (but less common) values.

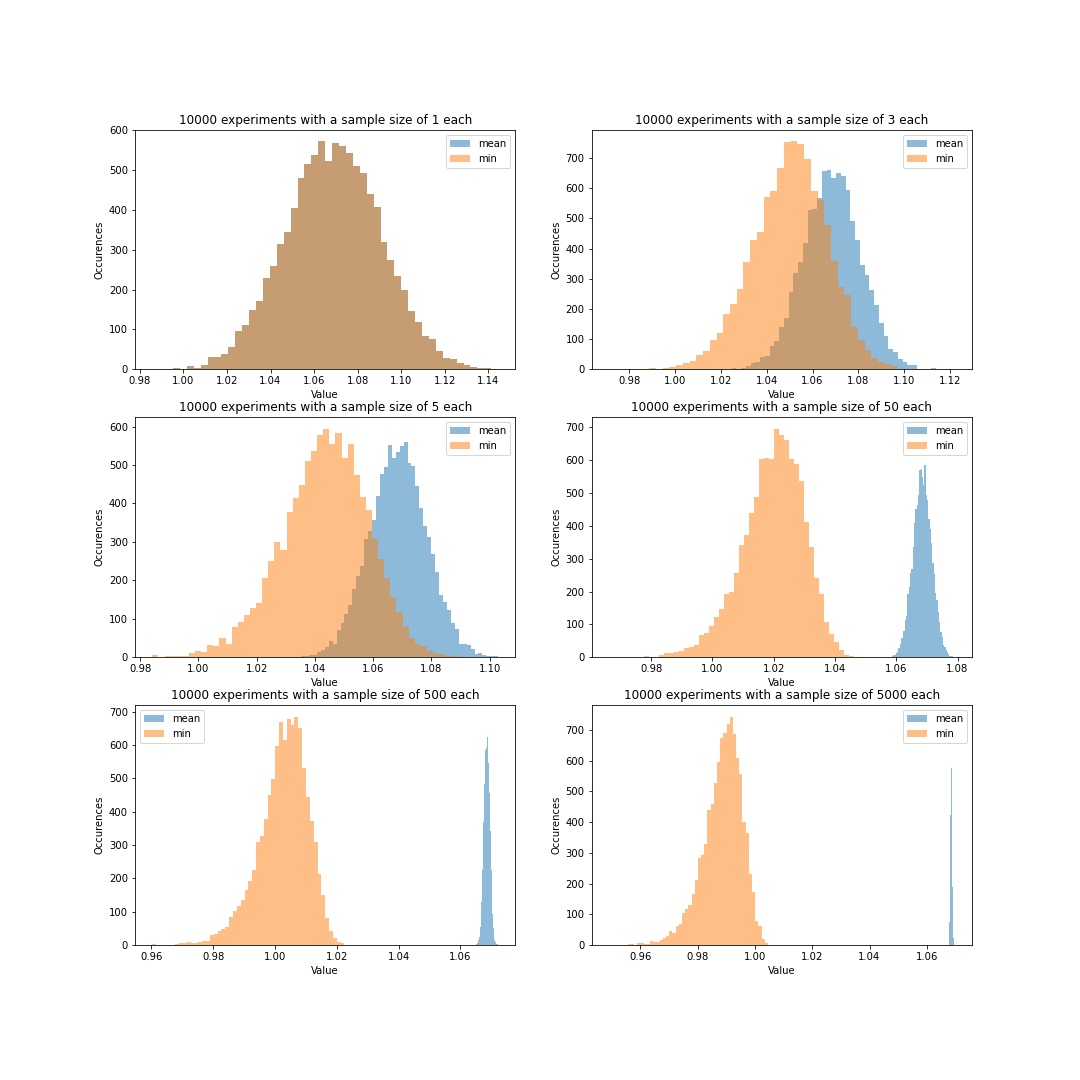
The precision seems to fall off with the sample size in both cases, but mean() performs noticeably better across the whole domain. This was visible in the above figure as well, as the histograms for min() were fatter than for mean().

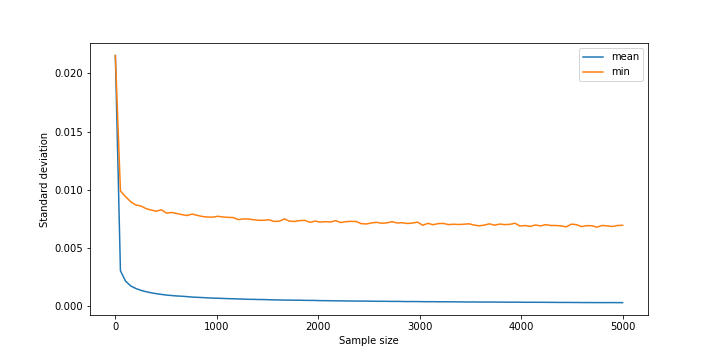
Overall there is no reason to choose min() in this scenario.

Execution time modeled by a Weibull distribution

A positive skewed distribution will pack more values to the left side, and thus intuitively min() should be less affected by the bias we previously saw. Indeed, if we look at the histograms for various sample sizes we see a much more timid bias towards smaller values. Moreover we start seeing a similar bias of mean() towards larger values.

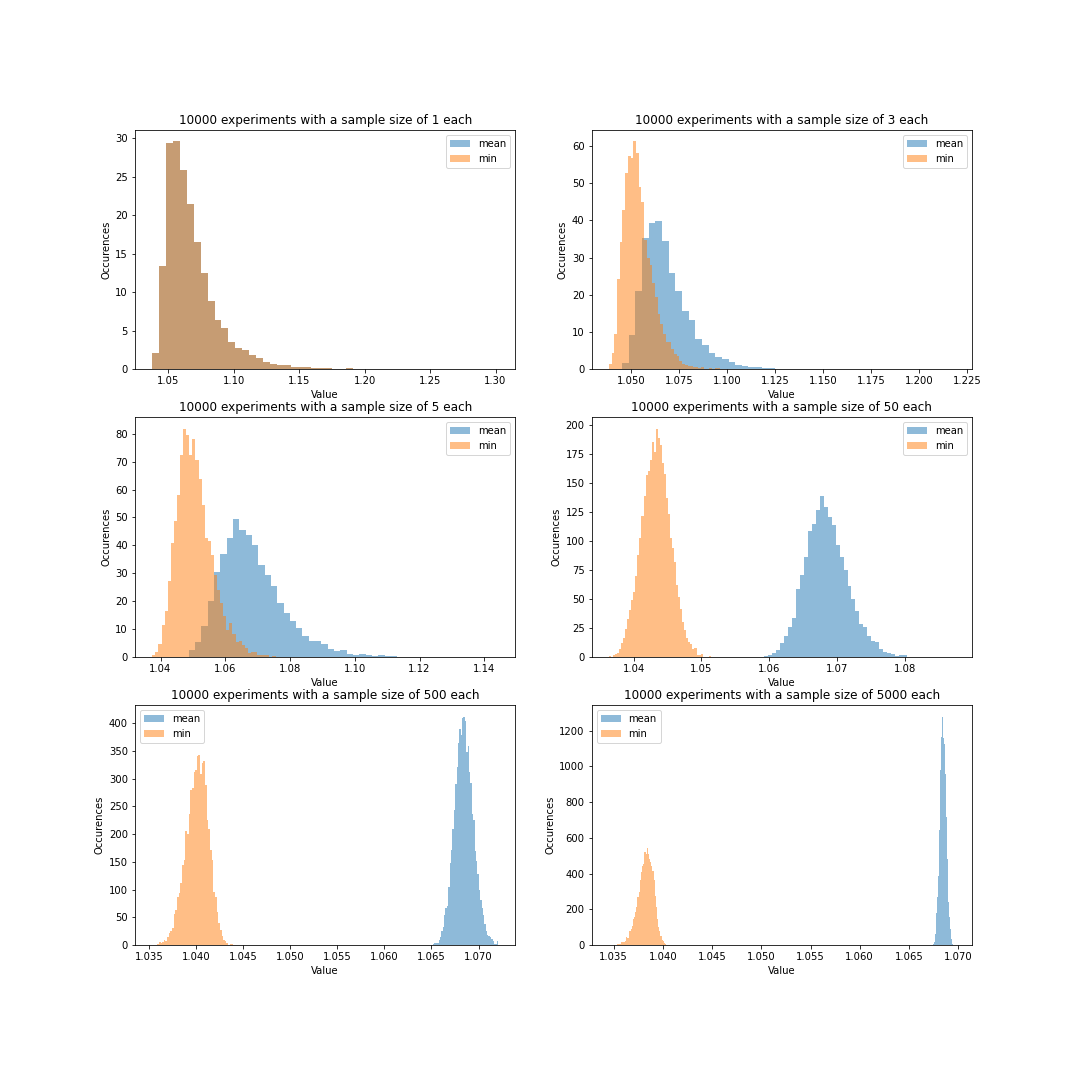
Interestingly enough, for smaller sample sizes, min() performs better in terms of precision, and while ultimately being outperformed by mean() the difference is much smaller than before.

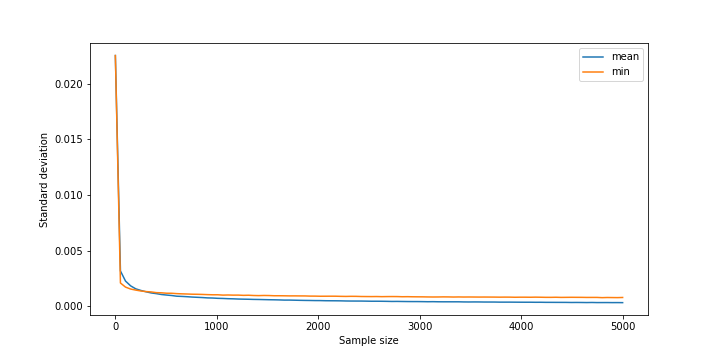
Arguably, for large workloads the better precision on small sample sizes makes min() the superior choice, thus blowing my mind and making me want to have shut up 😁.

A more detailed analysis would be interesting, specifically done by someone who knows their stats.